무브

오르비

아톰

내 태그

내 태그 설정

입시
학습
생활
클럽
직업·취업
Epioptimus
Centurion

논리화학 [746146] · MS 2017 · 쪽지

2021-08-03 18:00:31
조회수 6,159

논리화학의 최단경로 [2]

게시글 주소: https://simmen.orbi.kr/00038905343


개강 전까진 1주 2회(화/토 연재)로 바꿈.

개강후엔 쓰고싶을때 쓸듯



칼럼의 컨셉은 저번에도 말했듯이 '최단경로'임

'합리적이고 일관적이며 빠른' 풀이가 아니라 '최단경로'가 컨셉임을 유의하면 좋겠음

풀이가 좀 너무 발상적이라던가 내분을 너무 쓴다거나 그런 느낌이 들 수 있긴 할거임.

실제로도 시험장에서 모든 문제를 최단경로로 풀려고 하면 오히려 꼬이게 됨

그래도 적어도 기출문제에 한해선 최단경로 풀이를 혼자 생각해보고 알아두면 좋다고 생각해서 쓰기 시작한 칼럼임




칼럼 읽는 방법

1. 문제 사진을 보고 혼자 최단경로 풀이를 생각해본다 

(혼자 안 풀어보고 풀이 감상만 하면 도움은 1도 안되고 오히려 독이 됩니다)

2. 자신의 풀이와 칼럼의 풀이를 비교 해 보고 자기가 더 빠르면 댓글로 단다

3. 혹시 최단경로 풀이를 보고 싶은 기출문제는 문항넘버나 문제 캡처한 사진을 댓글로 단다



여기서 최단경로 풀이는 답을 맞추는게 아닌 증명을 의미함

예를 들어 문제에서 케이스가 두 개면, 반대편 케이스가 틀렸다는 증명도 풀이에 들어가야함

그러니깐 잘찍어서 푸는 풀이로 풀어놓고 댓글다는 이상한 짓은 ㄴㄴ


오늘은 양적 3개, 중화 1개를 준비해옴

오늘 양적은 일차함수 그래프 유형을 컨셉으로 잡았음

비킬러는 선별하기가 애매해서 댓글로 원하는거 달아주면 그거 해 드릴게요





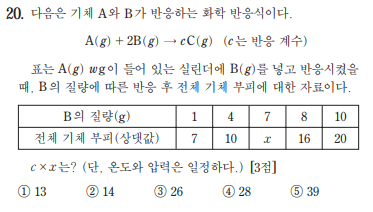
161120

스포방지용 간격




















최단풀이

1. B의 질량 (1~4), (4~8), (8~10) 각각의 변화량은 3, 6, 4이고 기울기는 1, 1.5, 2임. 투입유형의 성질을 생각하면 기울기가 3개가 나오려면 (4~8)구간에 완결점이 존재함.

2. 기울기가 1, 1.5, 2 이므로 기울기를 내분 해 주면 완결점은 6(4와 8의 중점)일때임

3. 완결점 이후에 그래프 공식은 투입한 B의 질량을 t로 두면 y=2t이고, x(B질량 7)는 완결점 이후이므로 x=14

4. 기울기 공식 (c-a)/b를 사용하면 (c-1)/2:1=1:2에서 c=2. 답 28



마지막 c 구하기 다른 방법 : 완결점 이전 일차함수 공식은 y=t+6임

t=0일때 y=6, 완결점인 t=6일때 y=12이므로 전체 기체 부피 2배 -> a:c=1:2에서 c=2





추가설명

나머지는 스킵하고

기울기 내분 사용법 : 밀도 내분하듯이 기울기를 내분하면 됨

위 문제에선 기울기 1이랑 2를 걸친 평균 변화율이 1.5였으므로 1:1내분한것

물리 예시) 1차원 상의 어떤 물체가 4m/s로 운동하다가 10m/s로 속력을 바꿔 운동했는데, 평균속도가 8m/s이다. 총 운동시간이 6초라면, 4m/s로 운동한 시간은?



풀이 : 8의 4와 10에 대한 내분비는 2:1임. 따라서 시간 비는 역수이므로 1:2, 4m/s로 운동한 시간은 2초


190919

스포방지용 간격





















이건 최단루트를 완벽히 이해하면 암산까지 가능한데, 대신에 중간중간 생각할게 좀 있고 일반적인 풀이 같지는 않음


최단루트

1. 그래프의 기울기가 완결점 전후 -3:1이므로 기울기 공식에 의해 a=5를 얻음.

2. 초기 부피가 y이므로, 완결점(B 5w)에서의 부피는 계수 비에 의해 2y/5

3. 반응 계수비를 보면 B:C=1:2이므로 이때까지 투입한 B의 부피는 y/5이며, 이게 5w의 부피임을 알 수 있음. 즉 B w당 부피가 y/25

4. 따라서 B 8w지점에서 전체 기체 부피는 2y/5 + 3y/25 = 13y/25. 이게 26이므로 y=50

5. B w당 부피가 y/25=2L이므로 B 20w당 부피가 40L, 즉 B 분자량 x=20w. 답은 5/2w


다른 최단루트

1. 기울기 공식에 의해 a=5

2. 0w지점에선 전체 기체 부피가 y. 계수 비에 의해 5w지점에서 전체 기체 부피는 2y/5

3. 일차함수니깐 내분으로 4w지점의 값을 구하면 됨. y와 2y/5를 4:1 내분하면 (5y+8y)/25=13y/25. 이게 26이니깐 y=50.

4. 완결점에서 부피는 20인걸 알 수 있고, B 3w를 넣었는데 6L증가했으므로 B 20w당 부피가 40L -> 분자량 20w. 답 5/2w

200720

스포방지용 간격






















설명 포함 최단풀이

0. 주의할점 : 미리 반응을 어느정도 시킨 상태에서 더 반응시키는 상황임 낚이면 안됨

1. (0~w), (w~2w), (2w~3w)의 변화는 -6, -2, 2. 구간 길이 같으므로 이걸 평균 변화율로 둬도 무방하며, 기울기가 세개가 나왔으므로 앞선 문제와 같은 논리로 완결점은 (w~2w)에 존재함

2. -2는 -6과 2의 중점이므로 기울기 내분 하면 완결점은 1.5w

3. 기울기 비가 완결점 전후 -6:2=-3:1이므로, 기울기 공식을 사용하면 a=5

4. 1.5w에서 전체 기체의 부피는 완결점 이전이나 이후의 기울기를 이용해서 계산하면 12, 계수 비에 의해 시작할 때 부피는 30

5. 21은 30과 12의 중점이므로, 과정 (가)에서 1/2반응지점까지 반응시킨 후 (나)에서 계속 B를 투입했다는 것을 알 수 있음.

6. 1/2반응지점까지 반응시키려면, A의 초기 부피가 30이므로 B는 부피 3 만큼 넣어주면 됨(6개 넣으면 완결점이니깐 절반 반응지점은 3개넣으면 됨). 따라서 n/m=1/10, a랑 곱하면 1/2





요약 : 기울기공식쓰면 a=5, 내분하면 완결점 1.5w, 1.5w일때 부피 12니깐 시작할때 부피 30, 21은 30이랑 12의 중점이므로 (가)에서 1/2반응지점까지 반응시킴, 따라서 m:n=10:1. 끝.



여기까지 포인트 : 일차함수 그래프 유형은 내분을 은근 많이 쓰게 된다. 잘 분석해보자

210920

스포방지용 간격























일단 들어가기에 앞서서 이 문제는 많은 학생(심지어 강사들 마저) 논리적 비약을 하며 풀고있음

다들 첨가한 산 용액의 부피가 V일때 (나)의 몰농도가 (다)보다 작으므로 (나)가 2가를 투입했다~이런 소리를 하는데

너무 당연한 반례 하나를 들면, 만약에 이 시점에서 (나)랑 (다)가 둘 다 산성이면 작은 쪽이 1가를 투입한거임

(나)에서 V일때 염기성이니깐 가능하지 않냐고 물어볼 수 있는데

(다)가 V일때 산성이면 또 모순 만들 수 있음

제대로 된 논증은 (나)와 (다)가 둘다 염기성이다 -> 중화점 이전에 1가 산을 투입하면 이온 수는 안변하는데, 2가 산을 투입하면 개수가 감소한다->따라서 (나)가 2가를 투입했다 이거임.



암튼 최단풀이


0. 염기성 용액에 산성용액 한 종류를 일정하게 투입하면 모든 이온의 몰 농도 합 그래프는 무조건 감소하다가 증가하는 개형을 가진다는 것을 상기하자(만약 산성용액 두 종류를 투입하면 감소하다가 일정하거나, 계속 감소하는 그래프 개형을 가지는 것도 가능함)

1. (나)에서 V와 3V일때 모든 이온의 몰 농도 합이 같으므로, 개형을 떠올리면 V일때 염기, 3V일때 산성이다.

2. (다)에서 V와 2V일때 모든 이온의 몰 농도 합을 비교하면 V일때 더 크므로, V는 확실히 염기이고 2V일때 액성은 알 수 없다(만약 V가 산성이라면 2V일 때 모든 이온의 몰 농도 합은 증가해야함)

3. (나)와 (다)가 V일때 둘 다 염기성이므로, 모든 이온의 몰 농도 합이 더 작은 (나)가 2가 산을 투입한 상황이다

----------------논증파트 끝--------------------

1. (다)에서 투입한 HA가 0ml, Vml일 때 모든 이온의 개수 합이 같아야 하므로 1*10=(V+10)*3/5을 풀면 V=20/3

2. (나)에서 3V(=20)ml을 투입했을때 이온의 양은 1/2 * (20+10)=15mmol. 2가 산과 1가 염기의 혼합이고, 액성은 산성이므로 15mmol의 1/3인 5mmol이 B2-의 양

3. HA와 H2B의 몰농도가 같으므로 (다)의 3V 시점에서 A-의 양도 5mmol

4. 반응 초기에 모든 이온의 양은 10mmol이므로 Na+의 양은 5mmol임. 즉 (다)의 3V시점에서 용액은 중성. 모든 이온의 양은 여전히 10mmol

5. 따라서 10/30=1/3이 답



설명 하나 : 2가 산과 1가 염기의 혼합 상황에서 염기일때, 산성일때 모든 이온의 개수 합 공식은 그냥 외워두자

산을 x개 염기를 y개 넣었다 치면

만약 산성이면 전체 개수는 3x가되고

만약 염기면 전체 개수는 2y-x가 됨

이걸 더 확장한 공식이 있긴 한데 내책에 있음 대충 캡쳐해옴


rare-다꼬리드디어세계지배 rare-Python

0 XDK (+0)

  1. 유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.

논리화학 [746146]

쪽지 보내기

  • 눈풀화1 · 900312 · 21/08/03 18:25 · MS 2019

    좋아요 0 답글 달기 신고
  • 눈풀화1 · 900312 · 21/08/03 18:39 · MS 2019

    190919 a=5 안쓰는 풀이 하나 얹자면
    0,0 5w,x를 이어주면 전 후 기울기가 2:1
    13w=26이 나오고, 26이 y와 20을 4:1내분점이라 y=50을 구하는 방법.
    그런데 a=5가 뻔히 보이는데 안찾고 푸는게 넌센스긴 하죠 ㅋㅋ

    210920 V = 20/3 안구하는 풀이 하나 얹자면
    액성 구한 후
    V지점에서 이온 수 비가 6:5
    중화점에서 이온 수 비가 4:3이니까 1.5V에서 2가 중화 -> 3V에서 1가 중화
    1가 염기에 산 용액 첨가, 혼합용액이 산성일때 전체이온수 = 첨가한 산 이온수
    따라서 3V지점 이온수비는 3:2
    y=1/3
    그런데 위랑 마찬가지로 V=20/3이 보이는데 안구한다는게 넌센스라 너무 뒷북스러운 풀이

    좋아요 0 답글 달기 신고
  • 논리화학 · 746146 · 21/08/03 18:44 · MS 2017

    첫번째껀 처음보네용
    두번째껀 알고는 있었는데 까먹고 안 적었네요ㅋㅋ 근데 안구하는게 넌센스긴하죠 풀이시간 비슷하기도 하고

    좋아요 0 답글 달기 신고
  • 공부하는람머스 · 1020642 · 21/08/03 18:44 · MS 2020

    좋아요 0 답글 달기 신고
  • Nx · 1075408 · 21/08/03 19:04 · MS 2021

    논화!논화!논화!논화!논화!
    좋아요 0 답글 달기 신고
  • 고칼슘쌀눈두유 · 1052683 · 21/08/03 19:10 · MS 2021

    6평 18번같은 순한맛 양적 빨리 푸는 방법이 궁금해요.. 그 문제를 19번보다 더 오래걸린듯

    좋아요 0 답글 달기 신고
  • 쿸쿸 · 903127 · 21/08/03 23:55 · MS 2019

    와 너무 유익해요!
    좋아요 0 답글 달기 신고
글쓰기
오르비 1348298번째 회원 가입
ddna
1,422,072 건의 게시물이
블록체인에 디지털 공증되었습니다.
901,751
497,321
22,267
574
159

오르비 캐스트

2025 수능D - 5

오르비 플레이

오르비 RARE

오르비 과외시장
Move
our corporate site
Orbi Class
on-line classes
Atom
educational books & resources
Gae9
humor and fun

© 2000-2024 Move Inc.

orbisoptimus (v17-38ba2b)